简介 采用了理论分析、工程估算、SPICE模拟以及与实际调试相结合的方法确定了射频接收系统中晶体振荡电路的结构、直流工作点及电路的元器件参数。
关键词 射频 晶体振荡器 SPICE模拟 工程估算
随着通信技术的快速发展,振荡器的研究、设计和技术得到了很大的发展。为了适应无线寻呼接收机、FM-SCA股票机、PDA等通信产品的小型化,在射频接收电路中一本振采用了晶体振荡电路。
一、 射频接收中晶体振荡电路的设计及工程估算
1. 振荡电路的确定
对振荡电路的选择取决于对工作频率、频率稳定度的要求,同时还要考虑射频接收小型化、低功耗及其他要求。晶体振荡电路应设计成结构简单、功耗小、调试方便并且频率可以微调的电路。经过分析,确定采用如图1所示的结构。该电路为电容三点式振荡,是串联式晶体振荡电路。
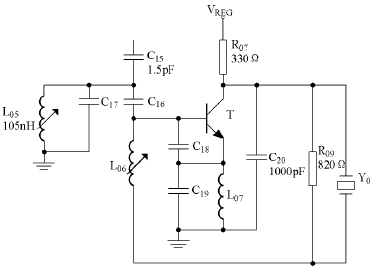
图1 一本振石英晶体振荡电路原理图
(1) 振荡电路原理分析
图2为图1的交流等效电路,其中C16、C17、L05组成的支路相对于三次泛音晶体的基频开路,在晶体的标称频率振荡时可以不考虑。由于振荡器的输出负载和振荡器之间是弱耦合,故也可以忽略不计。晶振工作在串联谐振频率上,且晶振发生串联谐振时,该振荡器电路的正反馈最强,只有这时才能满足振幅条件而使电路起振。一旦晶振工作点偏离串联谐振点,由于晶体的动态电感很大,而R09较小,则等效并联在电感和晶振两端的电阻较小,大大影响了谐振网络的Q值,使电路无法工作。
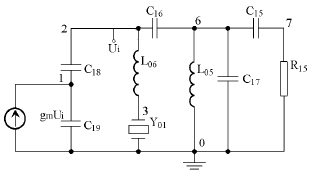
图2 交流等效电路
在此电路中,电路进入集电结的饱和区而发生饱和限幅失真,集电极电流因此包含丰富的谐波分量,输出负载网络调谐在振荡回路的二次谐波上(L06和晶振支路相对于二次谐波开路),而有效抑制基波及其余各次谐波。
此种类型的振荡器可以用如图3所示的模型描述,即一个线性时不变网络(LTIN)将振荡器电路分成三部分:一个非线性有源器件、一个基波谐振网络和一个二次谐波网络。
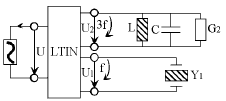
图3 一本振石英晶体振荡器等效电路模型
其中,有源器件的电流-电压转移关系可描述为:
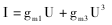
由于除了基波和二次谐波外,其他各次谐波没有可以流通的谐振回路,故为简化起见,分析时仅列出这两项(如上式所示)。在本电路中,二倍频选频回路与基波振荡回路之间属弱耦合,且二次谐波分量对振荡回路电流I的影响甚小,故U≈U1。因此,在分析此电路时,可先忽略二倍频选频回路,仅分析基波谐振回路与有源器件形成的网络回路,求出各点的基波电压幅度。由于该电路也会出现集电极饱和,因此集电极-基极电压被限幅,然后由图中基极-发射极电压与集电极各次谐波电流的关系得到集电极二次谐波电流,由此电流与二倍频选频网络组成的回路得出其二次谐波输出电压幅度。
(2) 频率稳定度分析
图4为由交流等效电路图简化后得到的振荡回路中基波回路的交流等效电路图。振荡器的环路增益可近似表示为AL=gmZL(C2/C1),其中ZL是L、C1、Y1和C2的并联阻抗,而Y1为晶体的等效阻抗,则频率稳定度为:
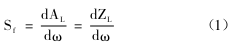
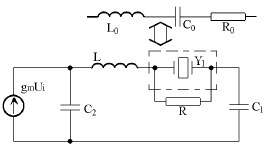
图4 振荡器的交流简化图
环路增益的极点有两对共轭解,频率为(式中C为C1与C2的并联电容),其中频率为ω01的极点位于右半平面,ω02的极点位于左半平面,故频率稳定度为
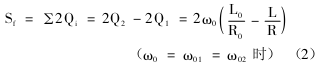
其中,Q2为晶体的品质因数,Q1为回路的品质因数,Q2Q1,所以Sf≈2Q2。由式(2)可知,采用上述振荡电路的频率稳定度极高,即振荡电路的振荡频率很稳定,有利于保证振荡频率的一致性。
调整L、C1、C2或由于温度等的变化使L、C1、C2值发生变化时,振荡频率的相对变化率为
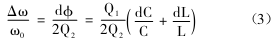
式(3)表明:晶体振荡器的频率在由晶振和外部调整网络共同构成的回路中,外部LC网络的Q值应该选择得比较低,才有益于晶体振荡器的频率稳定。
2. 晶体管的选择与静态工作点的确定
对小功率振荡器,晶体管的选择原则是能在工作频率范围内稳定地振荡。此外,管子除了应有足够大的跨导外,对于高频振荡器,其特征频率fT应大于振荡频率f。静态工作点的设定除了考虑起振和波形失真两方面要求外,还应考虑射频接收的低功耗要求。Motorola的晶体管MMBR911等即符合要求。图5为振荡电路的静态偏置电路。R07、R09分别为集电极和基极偏置电阻,静态工作点为Ub=0.7V、Uc=0.62V,集电极电流为1.30mA。
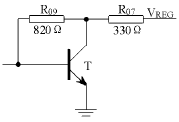
图5 静态偏置电路
3. LC回路参数与二倍频电路参数的确定
(1) 工程估算
以实际开发中的SCA股票机为例,假设接收频率为101.1MHz,第一中频为10.7MHz,则本振信号频率为90.4MHz。本振信号取自晶体振荡器的二次倍频信号,则该晶体的标称频率为45.2MHz。根据石英的特点,这种频段的晶体一般采用石英的三次泛音制成。
作为工程计算,当回路谐振时,图1中石英晶体可以近似地等效为纯电阻。振荡回路与二倍频回路的耦合是弱耦合,因此,在计算回路谐振频率时,可以忽略二倍频回路对振荡回路的影响。设C18=39pF,C19=10pF,则回路串联电容值主要决定于C19,计算时可以忽略晶体管参数Cbe。
下面计算回路谐振频率为45.2MHz时可调电感的中心值:
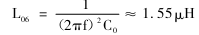
式中,
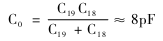
在实际使用中,由于寄生参数等的影响,L06的值还须实验校正或适当调整C19的值。同时,在各频段的电路调试中,若电容C18 和C19的值不变,则在不同频段L06的值应有所不同。电感值应由工程估算后,经实验确定。
在振荡电路中,发射极电感L07作轭流圈使用。它与C19组成的回路应谐振在三次泛音晶体的基频15MHz左右,以抑制振荡回路的基频分量,故可取L07=10μH,此时回路的谐振频率为
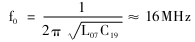
采用电容耦合取出振荡信号,通过二倍频网络的选频作用,在混频管基极得到所需的本振频率信号。二倍频电路由并联LC回路组成。设可调电感L05的中心值为105nH,当回路谐振在f=90.4MHz时,电容C17近似计算如下:
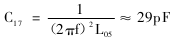
以上为振荡回路与选频回路的主要元器件的工程估算值,精确值还须实验调试确定。
(2) SPICE模拟
采用SPICE分析时,由于回路中有高Q值的石英晶体,在串联谐振点附近,电路对微分方程的不精确性格外敏感,最坏情况是正弦波在谐振点附近而又不在谐振点。这种情况下,SPICE误差控制公式不够严密,因此结果会不准确。
在进行SPICE模拟时,起初以工程估算值进行模拟,结果不太理想。后来,经过不断调整谐振回路参数,发现在L06=1.4μH、C17=24pF、C18=39pF、C19=10pF、L07=10μH时效果最好,其瞬态分析结果如图6所示(在模拟中晶振采用了近似短路模型)。
由图6可知:该振荡电路在约大于100ns的时间内就能稳定地振荡,完全满足射频接收中的预升起工作时间的要求;另外,二次谐波的频率较准,幅度远大于50mV,也能满足混频器对它的要求。
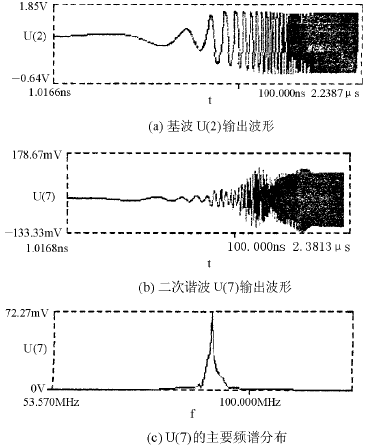
图6 一本振晶体振荡器瞬态分析结果
二、 实际电路中的振荡元器件参数
由以上分析所得的振荡回路及二倍频选频回路元器件参数运用到实际电路中进行测试,发现由于寄生效应的影响,这些元器件值并非最好:在确定了电感值的基础上,通过改变电容值使该电路的二倍频输出的频率为所需频率,并且其频谱较纯、幅度最大(在无高频信号输入的情况下用多功能综合测试仪测试混频输入级)。实验结果表明:当C17=22pF、C16=2.2pF、L06=1.2μH时,一本振的振荡频率为晶体的标称频率,且二倍频选频输出为100mV左右的二次谐波频率的正弦波。所以,在实际运用中射频接收中的一本振的电路我们选用了如图1所示的电路。
三、 提高振荡电路性能指标的方法
本地振荡电路的性能直接影响射频接收电路的总体性能,因此,从电路总体性能的要求出发,对本振电路提出的相应设计要求主要包括振荡信号的强度、杂波抑制、频率准确度、稳定度等。提高振荡电路性能指标的方法如下:
· 选用寄生响应比较高的泛音晶体。
· 提高振荡回路及选频回路的选择性。
· 在使用晶体时,应规定较大的寄生响应电阻比。一般三次泛音晶体应大于4∶1。
· 当晶体串联谐振频率ω1偏离回路谐振频率超过一定数量时,振荡信号强度变小,且出现畸变,杂波分量加大,这种情况应避免。
· 二倍频选频电路的频率响应也是影响振荡信号的强度及杂波分量大小的因素。因此,应选用高Q值电感,以提高回路增益及减小带宽。
最后,经实际测试,该振荡电路起振时间短、振荡幅度稳定且振荡频率可实现在晶振的标称值附近进行微调,其频率稳定度高且二倍频回路选频效果良好,幅度可达50~100mV,符合混频器对本振信号的功率要求。
参考文献
1 王国裕,陆时莹. SPICE-Ⅱ通用电路分析程序使用方法及其应用. 南京:东南大学出版社,1988
2 高文焕,汪蕙. 模拟电路的计算机分析与设计——Pspice程序应用. 北京:清华大学出版社,1999
3 Ferking M E著. 晶体振荡器设计与温度补尝. 杜丽冰,詹汉强译. 北京:人民邮电出版社,1985 |



